Notação de limites:
- lim f(x) = L
x->a
O que quer dizer? => "Quando x tende a 'a', f(x) tende a 'L'."
Analisando graficamente os limites de algumas funções:
Resolva exercícios e atividades acadêmicas
a)
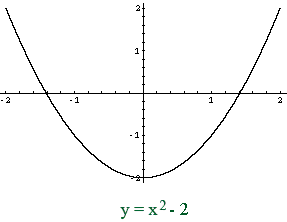
Se quisessemos saber o valor de:
lim f(x) ... Como descobrir?
x->1
tal que f(x) = x² - 2
Encontre o professor particular perfeito
Como não há nenhum "problema" nesta função. Ou seja, ela é contínua (podemos observar isto graficamente) no ponto em que desejamos calcular o limite, podemos analsar graficamtente o que ocorre com a função quando x se aproxima de 1. Nota-se que a função tende para algum valor. Que valor seria este? Podemos descobrir este valor simplesmente substituindo x por 1 na função.
Ou seja: f(1) = 1² - 2 = -1
De tal forma que
lim f(x) = -1
x->1
b) Limites laterais

Desejamos saber agora quanto vale:
lim f(x)
x->0
Graficamente podemos perceber que a função tende a -1 quando x se aproxima de 0 pela esquerda, em contrapartida podemos perceber que a função tende a 1 quando x se aproxima de 0 pela direita, ou seja, o limite lateral pela esquerda neste caso vale -1, enquanto o limite lateral pela direita vale 1.
Escrevemos da seguinte maneira:
- Limite lateral pela esquerda:
lim f(x)= -1
x->0-
- Limite lateral pela direita:
lim f(x)= 1
x->0+
Desta maneira podemos dizer que não existe o limite proposto acima. Já que os limites laterais possuem valores diferentes.
Ou seja:
lim f(x) não existe (neste caso)
x->0
Formalizando:
Existe 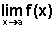 se e somente se ambos os limites laterais são iguais.
se e somente se ambos os limites laterais são iguais.
Pelo que estudamos neste item b. O que podemos dizer sobre o seguinte limite?
Verificando os limites laterais rapidamente, observamos que:
- Limite lateral pela esquerda vale menos infinito, pois quando diminuimos o módulo de x o falor tende a menos infinito, ou seja:
para x = -0,1 -> 1/x = -10
para x = -0,01 -> 1/x = -100
para x = -0,001-> 1/x = -1000
E assim por diante... Portanto:
- Limite lateral pela esquerda vale menos infinito, pois quando diminuimos o módulo de x o falor tende a menos infinito, ou seja:
para x = 0,1 -> 1/x = 10
para x = 0,01 -> 1/x = 100
para x = 0,001-> 1/x = 1000
E assim por diante... Portanto:
Assim chegamos a conclusão de que o limite pedido não existe, já que os limites laterais são diferentes;

