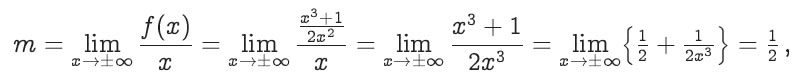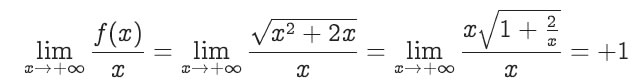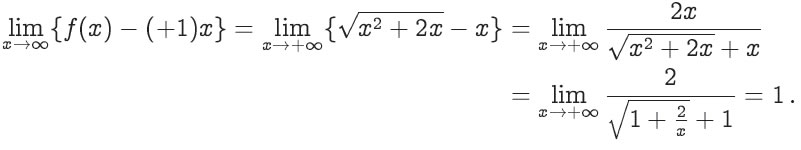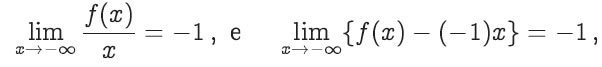Calcule o seguinte limite, caso exista:
limx?0sin(?x)sin(23x)limx?0sin?(?x)sin?(23x)
limx?0sin(?x)sin(23x)===limx?0sin(?x)xsin(23x)xlimx?0?sin(?x)?x23sin(23x)23xlimx?0?23sin(?x)?xsin(23x)23x.limx?0sin?(?x)sin?(23x)=limx?0sin?(?x)xsin?(23x)x=limx?0?sin?(?x)?x23sin?(23x)23x=limx?0?23sin?(?x)?xsin?(23x)23x.
Fazendo as mudanças de variáveis y=?xy=?x e t=23xt=23x, temos que
limx?0sin(?x)?x=limy?0sin(y)y=1limx?0sin?(?x)?x=limy?0sin?(y)y=1.
limx?0sin(23x)23x=limy?0sin(t)t=1limx?0sin?(23x)23x=limy?0sin?(t)t=1.
Onde nas últimas passagens usamos o limite fundamental do seno. Desse modo, sabendo que os limites existem, podemos substituí-los na expressão anterior:
limx?0sin(?x)sin(23x)===limx?0?23sin(?x)?xsin(23x)23x?2311?23.limx?0sin?(?x)sin?(23x)=limx?0?23sin?(?x)?xsin?(23x)23x=?2311=?23.
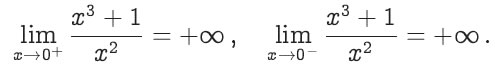
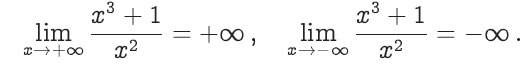
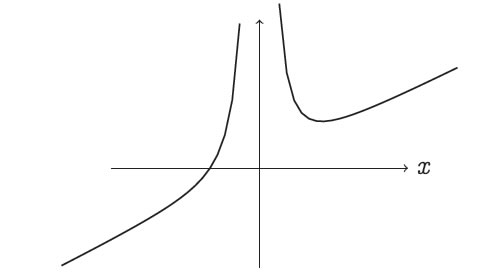
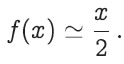
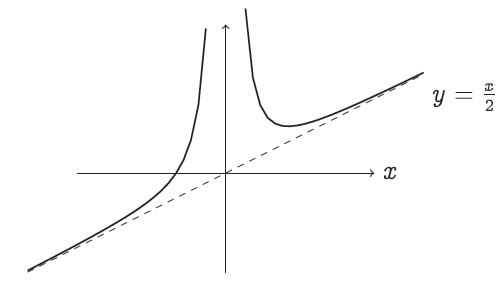
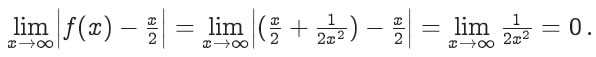 (5.33)
(5.33)
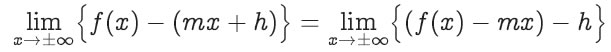
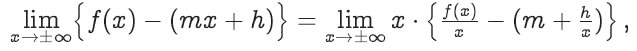
 (5.35)
(5.35)